Unit2-0 Q-learning Base

Unit1 이전글 Unit2 : Q-learning 원문

Value Function의 2가지 방법 §

• 우선 lr는 감가된 모든 reward에 대해서 최대값을 찾는 것으로 정의 한다.

$v_{\pi }(s)=E_{\pi }[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+2}+...|S_t=s]$

Abstract

Policy-Based method §

Policy-Based method에서 중요한 점은 직접적으로 policy에 대해서 훈련한다는 것이다. 예를 들어 특정 state에 대해서 action을 선택하고 해당 action이 얼마나 유효한지를 판단하는 것

Abstract

Value-Based method §

policy-Based와는 다르게 간접적으로 value를 평가할 수 있는 방법을 학습시키는 것이다. state || state-action pair를 학습하면서 value Function에 의해서 action을 찾는다. 이때 policy가 정해져 있지 않기 때문에 value function에 의해 가장 높은 reward를 가지는 action으로 Greedy한 정책을 선택한다.

이 때 value-based training은 최적은 value-function을 찾는 것이다. ${\pi }^{\ast }(s)=argmax{Q}^{\ast }(s,a)$ 여기서 exploration/exploitation trade off를 해결하기 위해 Epsilon-Greedy Policy를 사용한다.

---

Abstract

state-value function §

state-value function은 아래와 같이 정의된다. $V_{\pi }(s)=E_{\pi }[G_t|S_t=s]$ 수식은

1. s라는 state에서 policy에 따른 V(value)의 값은
2. 특정 state에서 기대되는 reward이다. 그림을 보면 간단한데 생쥐가 첫번째 칸에 이동 했을 때 목적지까지 얼마나 떨어져있는지를 수치적으로 계산한 것이다.

Abstract

action-value function §

action-value function은 아래와 같이 정의된다.

$Q_{\pi }(s,a)=E_{\pi }[G_t|S_t=s,A_t=a]$

state-value function과 비슷하지만 action에 대한 정보가 더 들어가게 되는 것이다

---

Bellman Equation : value의 추정을 단순화하자! §

state-value function을 쓰게 된다면 1번 정도의 게임에서 (episode라고 하자) 나오는 모든 reward에 대해서 알고 있어야 하고 이를 계산해야한다. 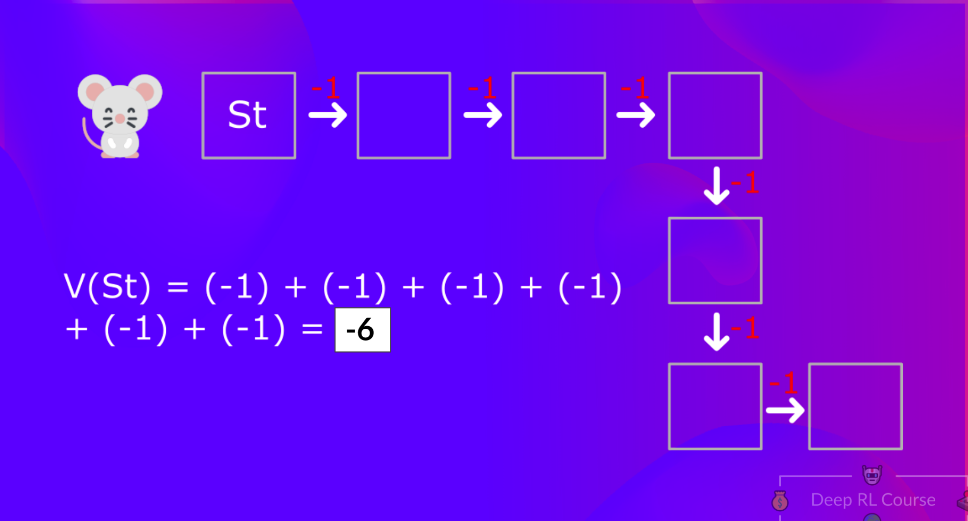예를 들어 첫칸에 들어갔을 때 치즈까지의 거리는 멀면 -1을 붙이게 된다면 -7이 된다. 이렇게 되면 너무 많은 시공간 복잡도를 가지게 된다.

이때 Bellman Equation을 사용하는데 Dynamic programming과 유사하다고 생각하면된다. 이는 재귀적으로 진행하면서 현재의 가치를 이 다음 reward 와 다음 가치를 통해서 업데이트 하는 것이다.

본문에서는 아래와 같이 얘기한다. $V_{\pi }(s)=E_{\pi }[R_{t+1}+\gamma \ast V_{\pi }(S_{s+1})|S_t=s]$

Example

즉각적인 reward에 할인된 다음 state의 값을 더해준다. §

이러한 개념으로 생각을 하게 되면 아래와 같은 그림이 가능해진다. 여기서 조금 중요해 지는 부분이 gamma 값에 관해서인데 gamma값이 커지면 미래의 가치가 현재에 조금더 크게 반영될 것이다. 예를 들어 gamma가 2가 되면 V(st)의 값은 -11이 되므로 현재 S에서 선택을 할때 미래의 가치를 좀 더 중요하게 생각하고 선택을 하게 된다.

---

그렇다면 여기서 생각을 해보는게 최초에 시작을 하는 상황이면 어떻게 되는거지? 난 V(s+1)을 모를텐데? §

라는 생각이 잠깐 들었는데 pass

---

Monte Carlo vs Temporal Difference Learning §

이번 페이지의 골자는 어떻게 value function을 Train할 것이냐에 대한 2가지 방법에 대해서 이다.

• Monte Carlo는 전체 episode를 경험하고 난 reward로 value를 결정한다.
• Temporal Difference는 각 step의 (현재 상태, 현재 상태에서 선택한 action, 다음 상태의 reward, 다음 상태)를 가지고 계산한다.

Monte Carlo §

몬테카를로는 전체 episode가 끝날 때까지 기다렸다가 reward(G)를 계산하고 value(V)를 업데이트한다.

$V(S_t)\leftarrow V(S_t)+\alpha [G_t-V(S_t)]$ Learning rate 이 alpha가 되면 현재 value(V)를 업데이트하기 위해서 모든 episode의 reward를 계산한다.

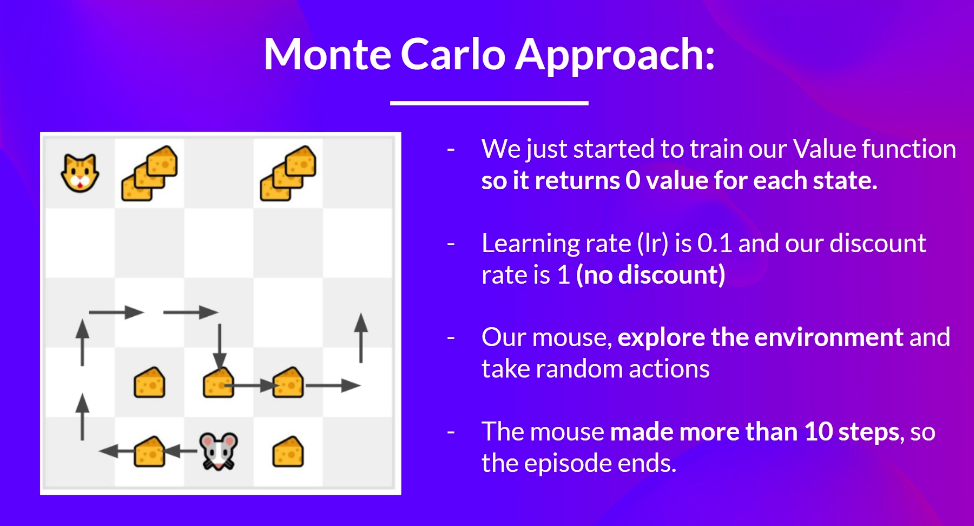
Example

예제를 들어서 생각해보면 전제 조건

1. 초기 value는 모두 0
2. learning rate := 0.1 -> 시간이 지날 수록 0.1씩 감소
3. 생쥐는 랜덤으로 움직인다.
4. 10번 움직이면 종료 혹은 고양이를 만나면 종료

이때 위 그림과 같이 움직였다면 G0 = 1+0+0+0+0+0+1+1+0+0 = 3 이 되고 V(S0) = V(S0) + lr * [G0 -V(S0)] 이며 V(S0) = 0 + 0.1 * [3 - 0] = 0.3 이되는 것이다.

Temporal Difference §

템퍼럴 디퍼런스는 한 step이 진행될때 마다 value를 업데이트한다. 하지만 우리는 전체 episode의 reward를 모르기 때문에 St+1의 reward인 Rt+1를 할인한 값으로 Gt를 추정한다.

이걸 여기는 bootstrapping이라고 한다. <- 전체 episode의 값이 아니라 추정하기 때문이다. 수식은 아래와 같다.

$V(S_t)\leftarrow V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]$

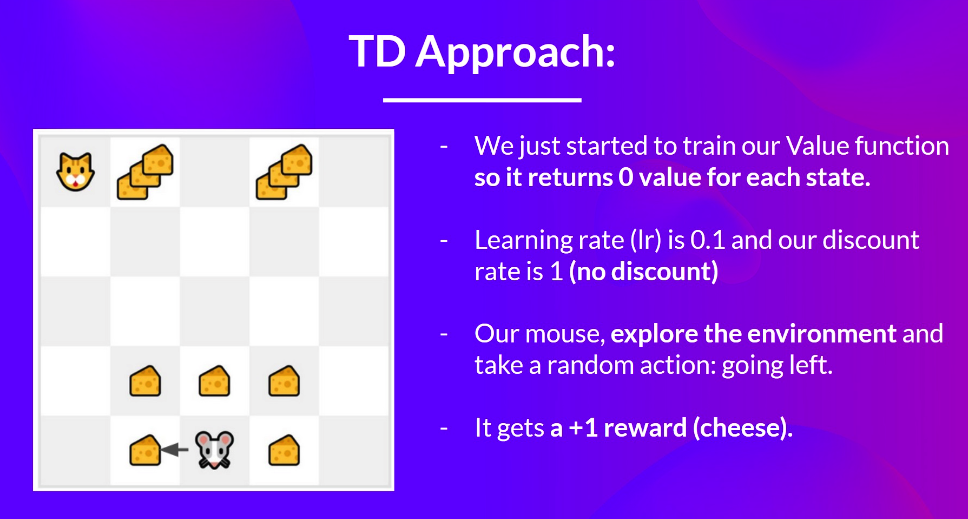
Example

비슷한 환경에서 V(S0)를 update해보면 V(S0) = 0(초기 가정값) + 0.1 (learning rate) * [1(다음 상태 reward) + 0.1(gamma) * 0 - 0] V(S0) = 0.1이 된다.

---

다음글의 Unit2-1 Q-learning과 함께